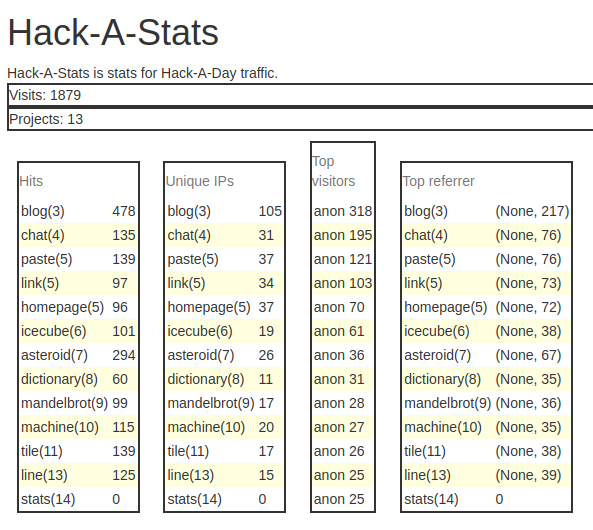
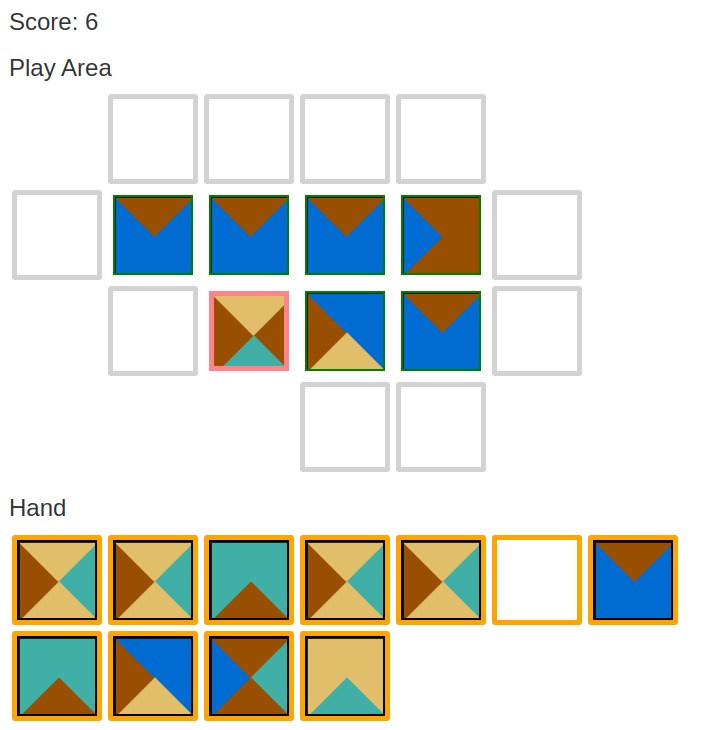
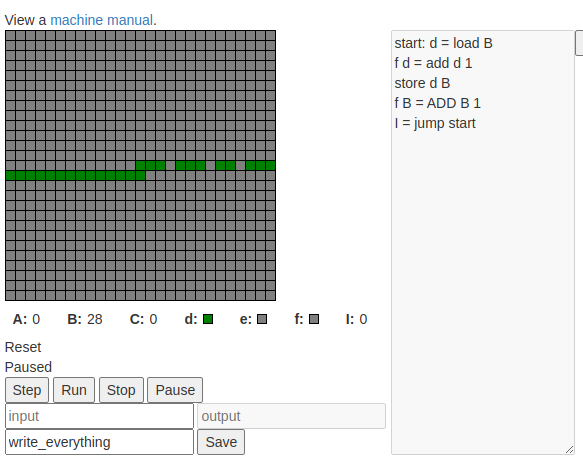
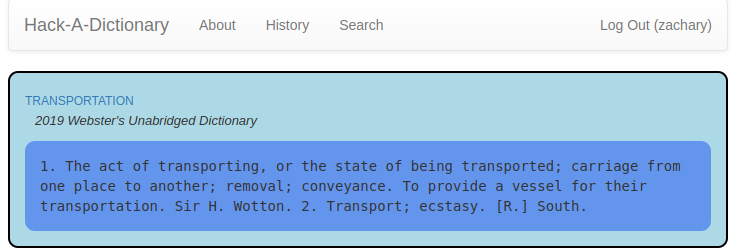
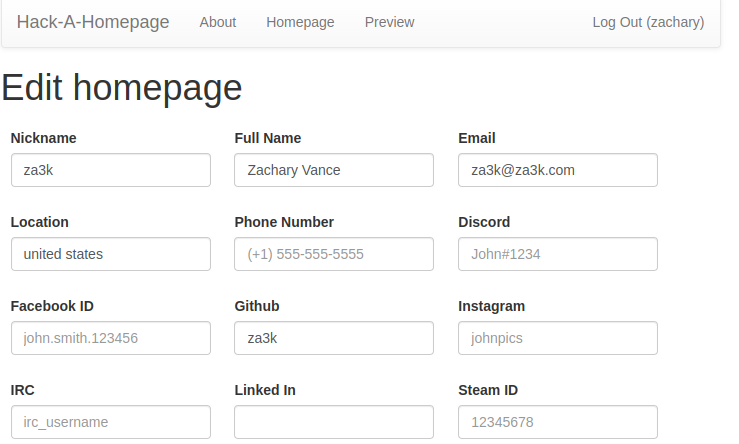
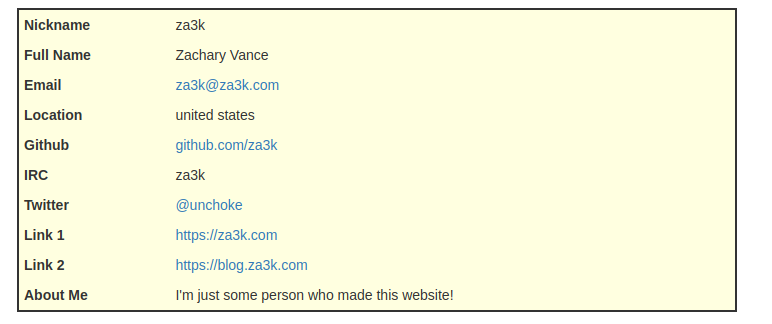
It’s november, and I’ve decided this month that I’m going to do 30 projects in 30 days. It’s an all-month hack-a-thon!
Today’s project is Hack-A-Sound (demo, source). It’s a small soundboard.
You can:
- Play 25 built-in samples
- Record your own samples with your mic
- Play samples directly, or record them on up to 4 tracks
- Have tracks play one time only, or loop
- Adjust the alignment of tracks
- Use a keyboard or mouse
- (Mobile not supported)
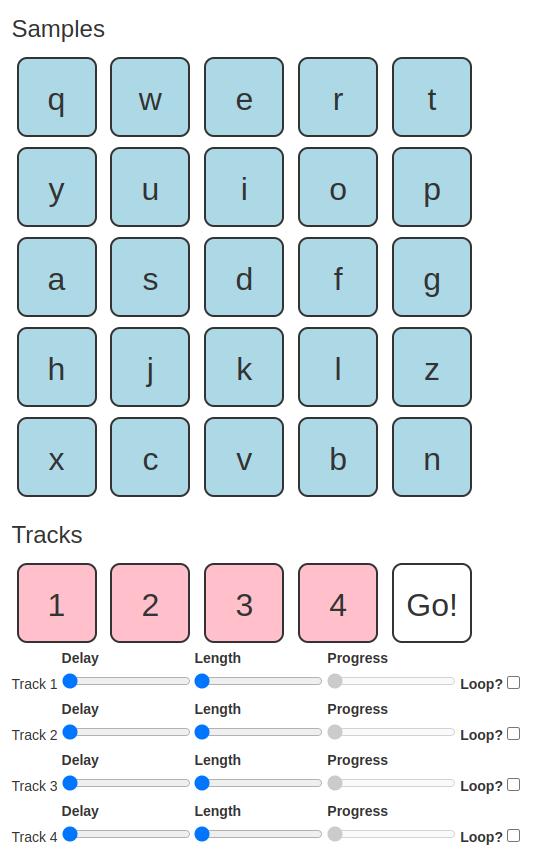
Have fun. I think this was a pretty good toy.