Lately I’ve been messing about in Godot, a framework for making video games (similar to Unity).
I wanted to make a 3D game. In my game, you live in a geodesic dome, and can’t go outside, because mumble mumble mumble poisonous atmosphere?.
A geodesic dome, I learned, is related to the icosahedron, or d20 from RPGs.



A simple dome is the top half of the icosahedron. As they get more complex, you divide each triangle into more and more smaller triangles.
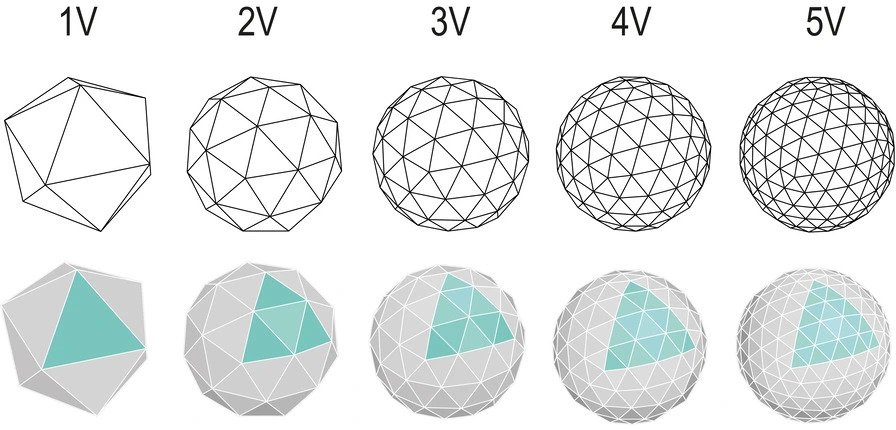
So to make a nice geodesic dome, we could find one (I failed), make one in Blender (too hard), or use some math to generate one in Godot. And to do that math, we need to know the list of 20 icosahedron faces. Which basically just needs the list of the 12 vertices!
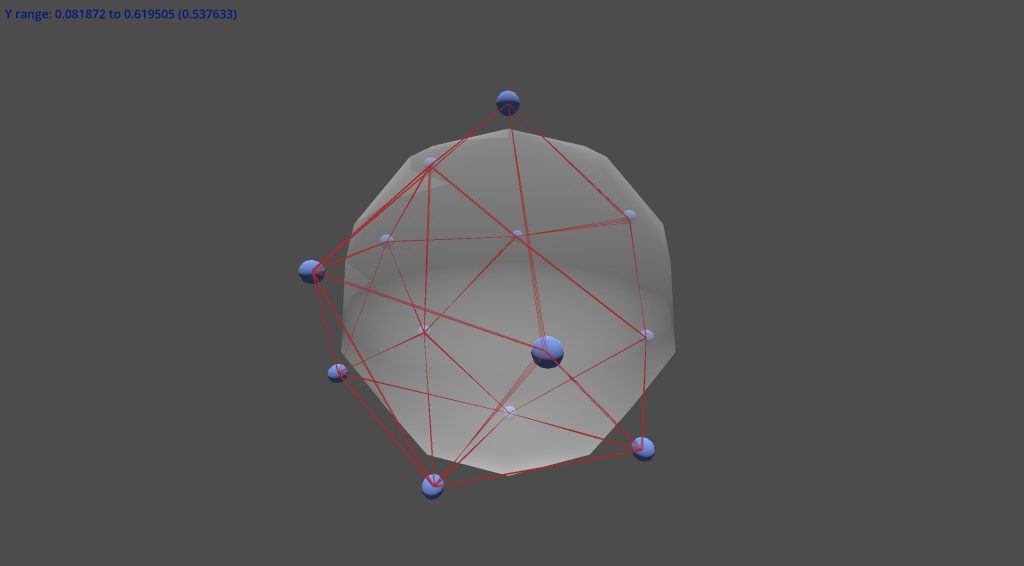
Now, obviously you could look up the vertices, but I thought of a more fun way. Let’s put 12 points on a sphere, make them all repel each other (think magnetically, I guess), and see where on the sphere they slide to. Maybe they will all be spaced out evenly in the right places. Well, here’s what it looks like:
So… kinda? It was certainly entertaining.
By the way, the correct coordinates for the vertices of an icosahedron inside a unit sphere are:
- the top at (0, 1, 0)
- the bottom at (0, -1, 0)
- 10 equally spaced points around a circle. they alternate going up and down below the center line.
(±1/√5, sin(angle), cos(angle)) [projected onto the sphere]
