The board game Go has been revolutionized in recent years by computer play. In 2016, AlphaGo beat Lee Sedol, a top Go player. This was the equivalent of what happened in Chess in 1997.
Since then, computers have continued to outstrip human players, but we have been learning a lot from Go engines. In this article I did some investigation using KataGo, which I understand to essentially be an open-source clone of the AlphaGo architecture.
This article assumes familiarity with the board game. If you're not familiar, I encourage you to give it a try sometime! Find a local try, or play online.
We have only one operation we can do. We can ask KataGo to analyze a position, and tell us how good that position is. That's the only operation we'll use in this article. And we're supposed to tell KataGo what the komi is.
KataGo returns two pieces of information for a position. An estimate of the score, and a percentage win chance.

The estimate of the score is determined (according to my very poor understanding), using an estimator which looks at the board, but doesn't try any moves. This is a fast, but low-quality metric.
On the other hand, the win rate is detemined by, simplifying some details, trying playing the game a bunch of times really fast and seeing how often black wins. It's slower, but more accurate.
Our first question is: How much should komi be?
Using only our one tool, let's figure out what KataGo thinks.
Well, in theory, what does a "good" komi mean? It means black and white should both win about 50% of the time. So let's just guess every possible komi, and find the one with the closest to 50% win rate.
Or, we could use the fast score estimator on an empty board with zero komi. If it thinks black is ahead by 6.0, maybe we could set komi to 6.0.
| size | komi estimate (winrate) | komi estimate (neural) |
|---|---|---|
| 3 | +14.0 | +4.4 |
| 4 | +0.5 | +2.4 |
| 5 | +25.5 | +23.3 |
| 6 | +3.0 | +4.3 |
| 7 | +8.0 | +8.7 |
| 8 | +9.0 | +6.6 |
| 9 | +6.0 | +6.0 |
| 10 | +6.0 | +5.6 |
| 11 | +6.0 | +5.5 |
| 12 | +6.0 | +5.5 |
| 13 | +6.0 | +5.6 |
| 14 | +6.0 | +5.5 |
| 15 | +6.0 | +5.7 |
| 16 | +6.0 | +5.8 |
| 17 | +6.0 | +5.9 |
| 18 | +6.0 | +6.1 |
| 19 | +6.5 | +6.2 |
It turns out both methods give similar results. We're going to use the win rate method going forward, because in general I've been told it's more accurate for many board positions.
In fact, we can use the same method to evaluate any board position accurately. We can figure out what komi would make that board position 50-50 for white or black to win. And then we can treat that as the "value" of the position.
For the rest of the article, we're going to simplify, and only ask the value of board positions. We don't care which method we use, but I'll mark the fast-and-simple method as "neural", and the winrate method as "komi" or "winrate" in pictures.
Our next question is, what are different starting moves worth? Well, let's just play every one and see what KataGo says the score is.
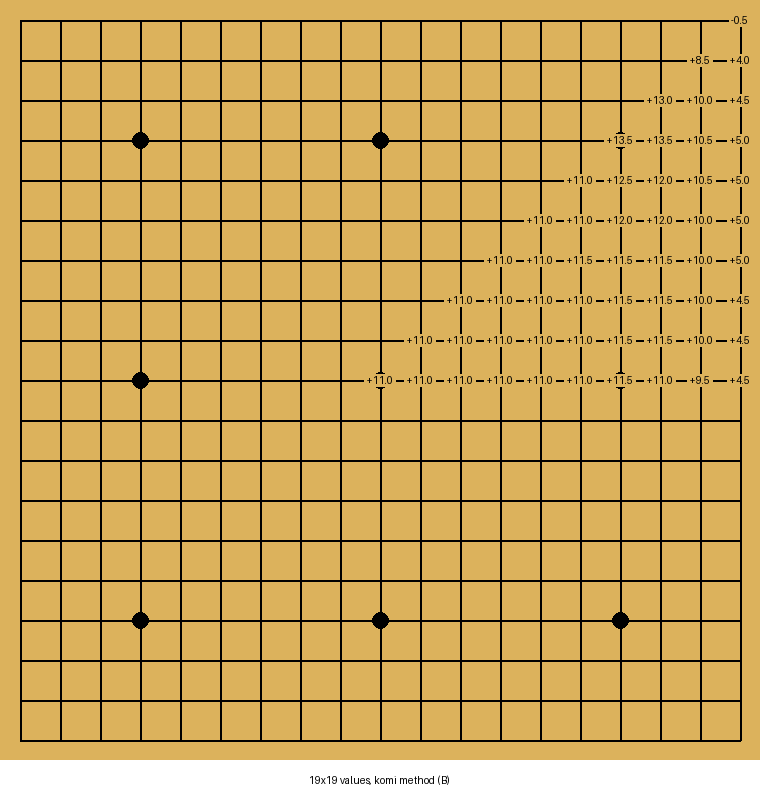
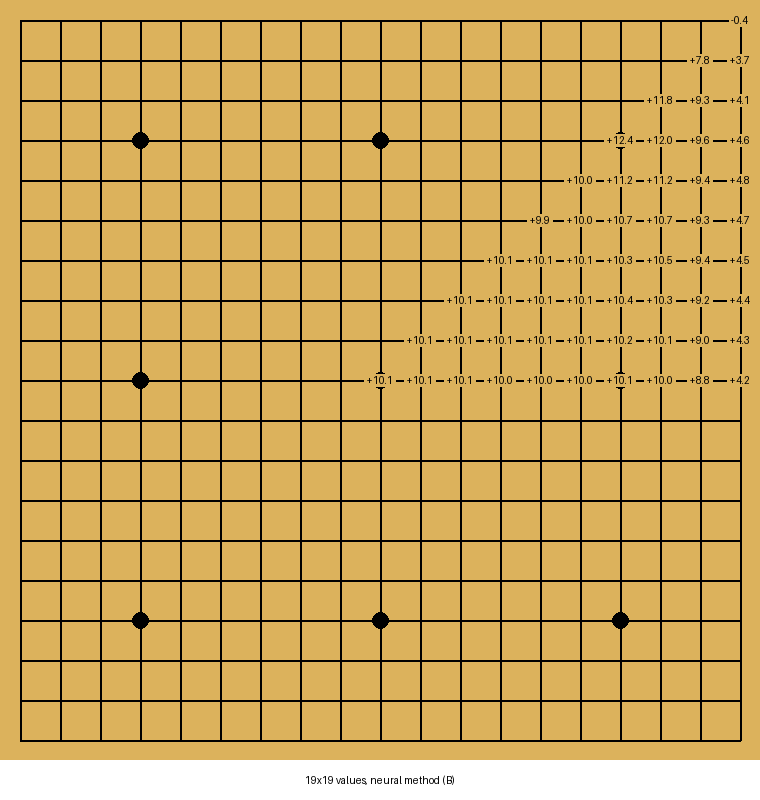
Note that all scores are relative to +6.5 for the empty board, which is why some values are negative.
Okay, easy enough. What about different numbers of handicap stones? Using standard placements, we get:
| size | handicap | value estimate (winrate) | value estimate (neural) |
|---|---|---|---|
| 19 | 1 | +6.5 | +6.2 |
| 19 | 2 | +20.0 | +19.2 |
| 19 | 3 | +32.5 | +32.5 |
| 19 | 4 | +47.5 | +46.6 |
| 19 | 5 | +59.5 | +58.3 |
| 19 | 6 | +72.5 | +71.8 |
| 19 | 7 | +86.0 | +85.1 |
| 19 | 8 | +100.5 | +100.3 |
| 19 | 9 | +115.5 | +114.7 |
| 13 | 1 | +6.0 | +5.6 |
| 13 | 2 | +19.5 | +18.6 |
| 13 | 3 | +32.5 | +30.7 |
| 13 | 4 | +48.0 | +47.4 |
| 13 | 5 | +59.0 | +58.6 |
| 13 | 6 | +75.0 | +74.5 |
| 13 | 7 | +87.0 | +84.0 |
| 13 | 8 | +100.5 | +96.1 |
| 13 | 9 | +109.5 | +102.3 |
| 9 | 1 | +6.0 | +6.0 |
| 9 | 2 | +16.0 | +16.0 |
| 9 | 3 | +27.5 | +27.1 |
| 9 | 4 | +75.0 | +53.5 |
| 9 | 5 | +74.5 | +79.0 |
Now let's make things more spicy. I keep winning every 1-stone game, but losing every 2-stone game. I want a 1.5 stone handicap. Well we can't add fractional stones, but we can look for something worth between 6.5 and 20 points.
Or, let's find something worth 0.0 points. I want a board position we can start with and not need that dumb komi rule.
Let's do the full analysis. Every possible starting board positions. Then we'll look for one that KataGo says is worth around... say, 12 points.
Of course, we can't really analyze every board position, so I just did ones with up to 2 stones. I included ones with white stones, because why not?
Here's what the ones with two black stones on 19x19 look like. It might take a bit to load, and you'll need to zoom in.
The full set of pictures is online.
- 19x19, 1-stone positions (black) winrate neural
- 19x19, 1-stone positions (white) winrate neural
- 19x19, 2-stone positions (black-black) winrate
- 19x19, 2-stone positions (black-white) winrate
- 19x19, 2-stone positions (white-white) winrate
19x19, positions closest to exact point values winrate
- 9x9, 1-stone positions (white) winrate neural
- 9x9, 2-stone positions (black-black) winrate
- 9x9, 2-stone positions (black-white) winrate
- 9x9, 2-stone positions (white-white) winrate
- 9x9, positions closest to exact point values winrate
You can also get the raw score of 2-stone (and lower) positions on 9x9 and 19x19 boards. The code to do analysis and generate the pictures is on github, as are details on exact software settings used.
Thanks to Google for AlphaGo, and to lightvector for Katago (and Katago support).
Addendum.
After doing this project, I found it had already been done (better) at katagobooks.com. Apparently what I've done is called an "opening book", even if my goal was a bit different.
